号)から対称性の導き方と空間群の分類を説明した.今 回はミラー指数,ラウエ指数の定義および実験で得られ る消滅則の厳密な関係を紹介する.日常的に使われる概 念であるにもかかわらず意外と誤解が多いと感じている.ミラー指数とは 以下,ウイキペディアの解説です. ミラー指数は結晶の格子中における結晶面や方向を記述するための指数である.英国の鉱物学者ウィリアム・ハロウズ・ミラー(William Hallowes Millor)によって考案された.ミラー指数には,面指数と方向晶の方向を表したいときもあります.結晶の方向は「面に垂直な方向」と表すので,面のミラー指数表記 が分かっていれば簡単です.この記事では,方向を表すときのミラー指数についていくつかの例を紹介し ます. 結晶の方向の表し方
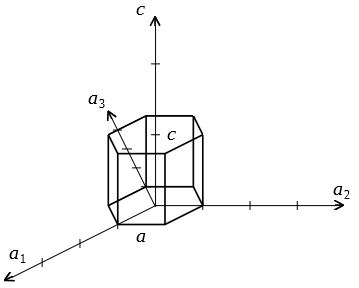
ミラー指数による立方晶 六方晶における面と方向の表し方
ミラー指数 方向 表し方
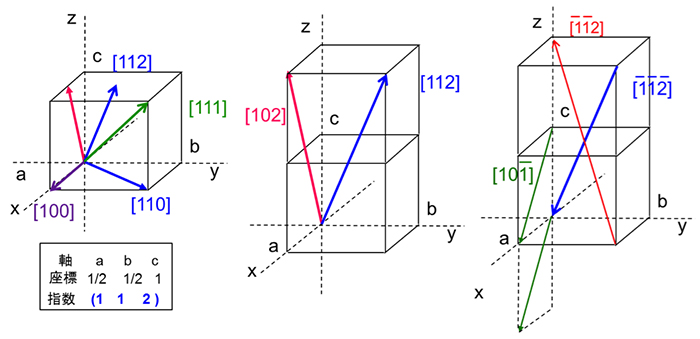
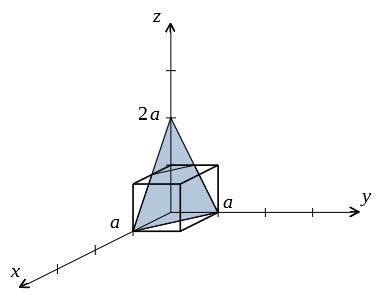
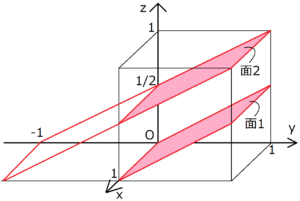
ミラー指数 方向 表し方-この面のミラー指数は と表記し,「ろく・さん・に・めん」と読みます. 交点がマイナス方向で座標軸を切ったときは指数の上に を付けて表記します. 上の図のように 軸を それぞれ で切る場合は となります. 読み方は「に・いちばー・に・めんミラー指数の決め方 とある格子面のミラー指数は、その格子面を無限に延長させたときのx,y,z軸の切片の逆数で表せる。下に具体例を挙げる。 例題 (1,0,0) 上の図の赤く塗られた格子面のミラー指数を考える。 まずx軸の切片は明らかにx=1である。
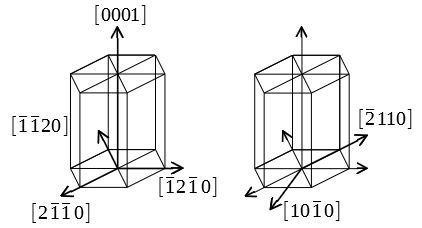



ミラー指数による立方晶 六方晶における面と方向の表し方
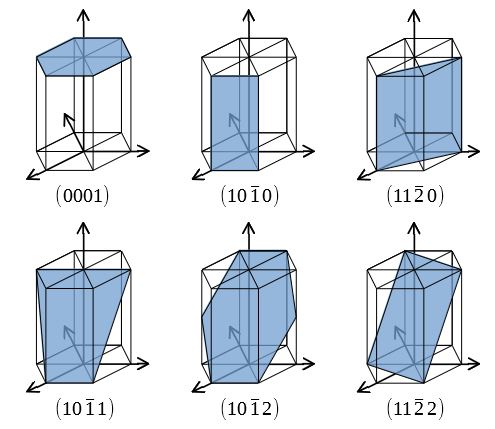
ミラー指数 463 六方晶におけるミラー指数 六方晶における主要な面 底面 錐面 柱面 8 六方晶における主要な方向 Polar Stereographic Polar Stereographic Equatorial Stereographic Oblique Stereographic 結晶方位の表し方AF や AC は A を原点としているので分かりやすいですね. それぞれの方向に垂直な面を ミラー指数(面) の手順で表わし角括弧で括れば, AF は ,AC は となります. DB の方向については,DBに垂直な面が そのままではミラー指数で表し辛いので,一見良く日本大百科全書(ニッポニカ) ミラー指数の用語解説 イギリスの鉱物学者W・H・ミラーが結晶面の記号として19年に採用したもの。天然の鉱物結晶や実験室で溶液から成長させた結晶は、普通、平面によって囲まれた規則正しい多面体の外形をもつ。この外形に現れている平面を結晶面という
この面のミラー指数は と表記し,「ろく・さん・に・めん」と読みます. 交点がマイナス方向で座標軸を切ったときは指数の上に を付けて表記します. 上の図のように 軸を それぞれ で切る場合は となります. 読み方は「に・いちばー・に・めん」です.結晶格子面の表し方 平行で等間隔な格子面の組 格子面が3軸を切る点をA, B, Cとし、原点Oからそれらの点に至る距離 をOA, OB, OCとする 格子点 r ua vb wc u, v, w 整数 a b c O A B C a h OA cc b k OB c l OC で与えられる h', k', l' は有理数である。 h', k', l' に適当71 ミラー指数: ミラー指数の表し方 ・任意の方向の表し方 ①その方向と平行でかつ原点を通る直線 OP を 引き,OP 上の任意の点の座標 (x, y, z)を求める. ②座標 (x, y, z)を各格子定数で除した値 (u, v, w) を求める. c z w b y v a x u , ,
TD方向をβ=0としているので、 測定時、RD方向をビーム方向に合わせる 試料の回転方向はCWなので、 データの並びは、CCW方向である。 Rigakuの極点図 測定時、RD方向をミームに対し90度とし、極点図の 外側から測定を行っている。5 ・2格子面の同定 (a)ミラー指数 任意の面の表し方 (1)面と各軸との交点座標(x,y,z)を求める. (2)座標(x,y,z)を各格子定数で割った逆数(h,k,l)を求める. (3)座標成分を最小整数比に直し,括弧にくくって表す.17年10月06日現在 収録数 8,004記事 記事;
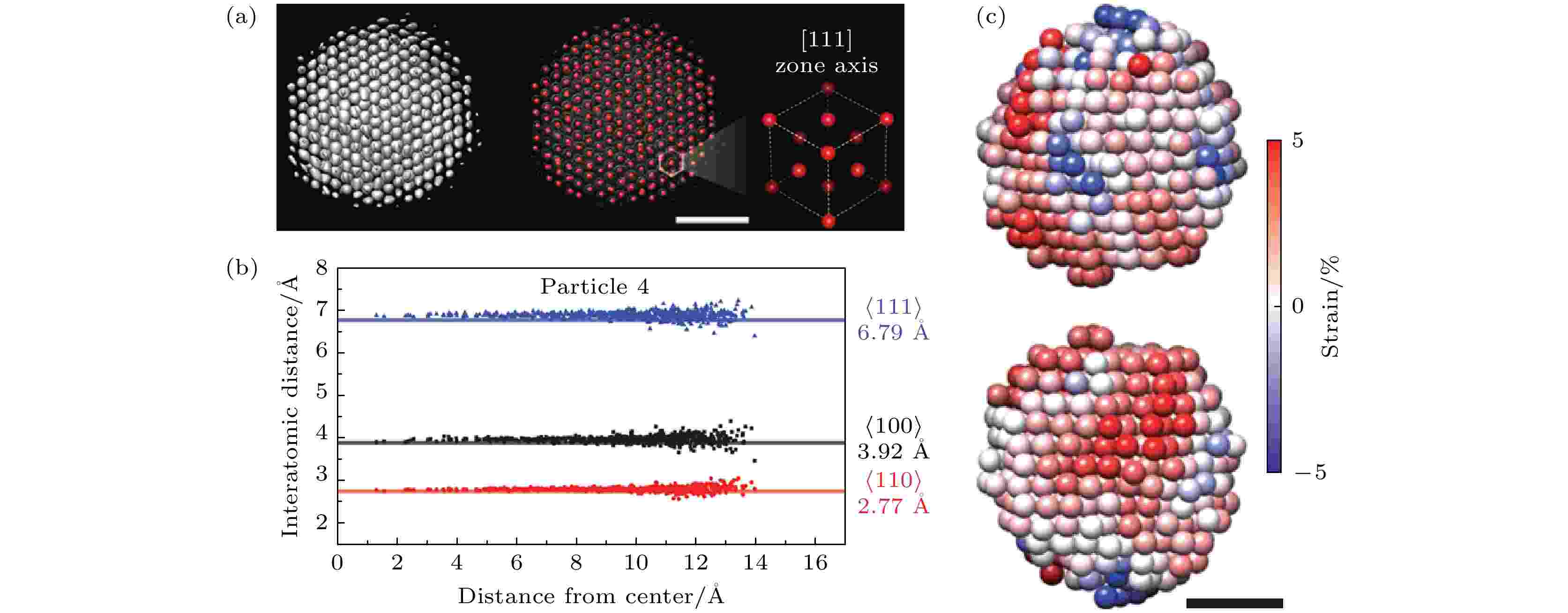



Atomic Scale Characterization Of Three Dimensional Structure Magnetic Properties And Dynamic Evolutions Of Materials By Transmission Electron Microscopy



半導体物理 結晶構造 3 ミラー指数 Sciencompass
ミラー指数で表された面の図の書き方 ミラー指数が(111)の面 ミラー指数が(121)の面 ミラー指数が(101)の面 ミラー指数で表された面の図の書き方 ミラー指数がの面を図示する場合は、次のとおりである。 まず、結晶中の座標軸を、互いに独立な3つのベクトルで表すと考える。 の場合、 のこの記事では,六方晶系の面指数・方位指数における4指数3指数の対応関係について備忘録として簡単にお話しさせていただきます. 六方晶系ではa1軸, a2軸, a3軸, c軸の4つの結晶軸 (図2 (右))と対応した4指数を用いる場合がほとんどです. ( ) 六方晶は6回固体物理学における基本となる ミラー指数について解説しました。 線方向の表記や面指数 3指数と4指数の変換など 金属 マテリアル ミラー指数 大学 材料 専門 固体物理 固体物理学 3指数 4指数 この著者の他のノートを見る このノートが参考になったら



ミラー指数が 101 のとき格子面が図のようになりました この Yahoo 知恵袋



ミラー指数 方向 物理のかぎしっぽ
構造説明文中の{1 0 0}や1 1 1>などは、結晶面および結晶中の方向を示すミラー指数と呼ばれる指標です。3つの整数 h, k, l を用いて (h k l)、{h k l} が結晶面を、h k l、<h k l>71 ミラー指数: ミラー指数の表し方 ・任意の方向の表し方 ①その方向と平行でかつ原点を通る直線OPを 引き,OP上の任意の点の座標(x, y, z)を求める. ②座標(x, y, z)を各格子定数で除した値 (u, v, w) を求める. c z w b y v a x u = , = , =上図に示すような単位格子ベクトル a, b, c を持つ結晶系で, と表し, ミラー指数 と呼ばれます。 ここで,ある座標軸方向と平行で交点を持たない場合は,その軸と無限遠(∞)で交差するとし,その指数は 0 と約束します。 例えば,各座標軸と 1,1
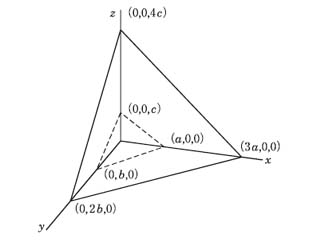



ミラー指数とは コトバンク



2
結晶面の指数 hkl方向とは・・・a 1 a 2 a 3 (hkl)面とは・・・a 1方向に1/h, a 2方向に1/k, a 3方向に1/l, で定義される3点を含む平面 h 1 k 1 l 1 r ha 1 ka 2 la 3 ベクトルrの方向 rに意味はない r hkl方向ミラー指数 (面指数) 結晶は結晶面という特徴的な面で切って考える事が多いですが、この結晶面は逆格子ベクトルというものと対応しています。 今回は、ミラー指数について説明してみました。 結晶面は実空間に描けるのでイメージしやすいですが結晶の面については、ミラー指数が用いられます。これは格子定数 に対して各軸と の位置で交わる点を結んでできる面を と表します。 六方晶の場合は方向、面ともに、指数 を導入したミラー・ブラベー指数により表されます(図24)。




Pdf Refraction In Planetary Atmospheres Improved Analytical Expressions And Comparison With A New Ray Tracing Algorithm



437円 66 Off 半額 半値以上 55 Off扇珠館 Xl 30u ギフト プレゼント 出産 内祝い お返し 結婚 法事 人気 ご挨拶
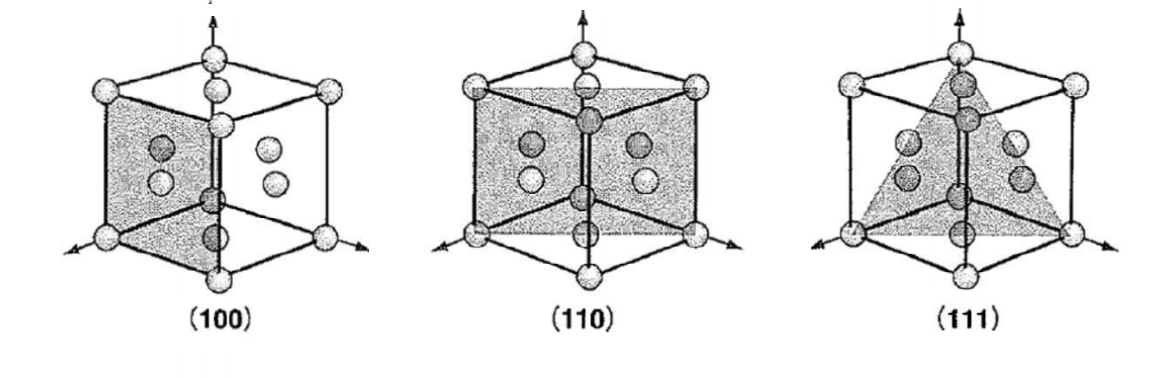
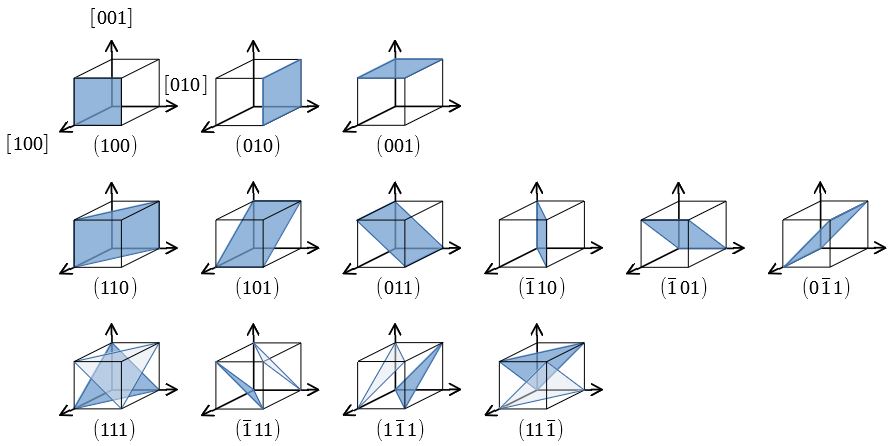
ミラー指数(面) 5 仮に,上の単位格子が立方晶だとすると(100),(010),(001) は等価な面です.立方体はa,b,c どの軸で も90 度回せばもとにもどりますから,(100) の図をc 軸の回りに90 度回せば(010) の図になります. (010) の図をa 軸の回りに90 度回せば(001) の図になります.図にはありませんミラー指数 ミラー指数の表記 六方晶におけるミラー指数 六方晶における主要な面 底面 錐面 柱面 7 六方晶における主要な方向 Polar Stereographic Polar Stereographic Equatorial Stereographic Oblique Stereographic 結晶方位の表し方ミラー指数は結晶格子の面や方位を表すために広く使われている表記法で、次のようなルールにしたがって表します。 ミラー指数 表している面または方位 軸を する点を結んで作られる面。 軸の負の方向に する点, 軸を する点を結んで作られる面。 は



2



ミラー指数 方向 物理のかぎしっぽ
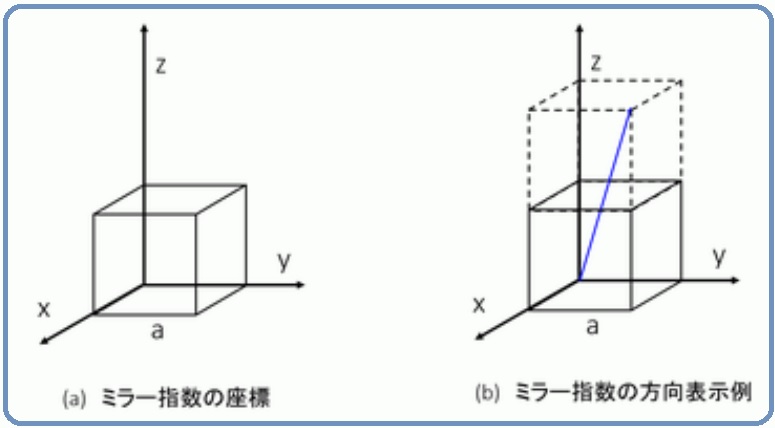
ミラー指数に( )が付いているのには、ちゃんと意味があります。 (hkl)は、面を表します。 {hkl}は、(hkl)と等価な対象性を持つ面全てを表します。 hklは、(hkl)の方向を表します。 は、(hkl)と等価な対象性を持つ面の方向全てを表します。 上の図に戻ります。ミラー指数(方向) 3 DB の方向については,DB に垂直な面がそのままではミラー指数で表し辛いので,一見良く分かりま せん.結晶軸はどこにとっても差し支えないので,つぎの図のように考えましょう. こうすれば,DB に垂直な面はa 軸に1 で,b 軸に¡1 で交わることが分かりますから,面の図1 ミラー指数の方向の表示方法 図2にミラー指数の方向として頻出する方向を示します。 これらはすべり系の方向としてもよく出てきます。 また面のように対称性のある等価な方向の表示としてはカッコの形状を<>にして<112>として表示します




Pdf Refraction In Planetary Atmospheres Improved Analytical Expressions And Comparison With A New Ray Tracing Algorithm



2
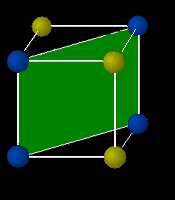
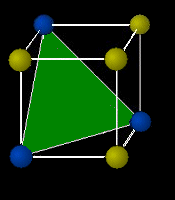
図3 ミラー指数 単位格子の外形や格子点の並びで構成される格子面あるい は、結晶の原子で構成される原子面を表す方法にミラー指数と 呼ばれるものがある。面の方程式に倣って切片を利用する方法 である。面の方程式は、 AxByCz= 1ミラー指数とはなにか? 結論からいうと、 ミラー指数は結晶面とその方向を記述するためのものです。 結晶面というとイメージが湧きづらいかもしれませんが、 単位格子が"ブロックでの繰り返し"で結晶を記述していたのに対して、 結晶面は"面立方晶の面指数(ミラー指数)についてです (基本的な作り方は面心立方晶(fcc)なら↑のような切り方をしたときに切り口が違う形を選びます。) それでも無理やり4つ目を作るなら、bcc、fccであれば上記に加え{0}とかあってもいいような気が。




Jpa Microfluidic Device Google Patents



ミラー指数についての質問です 写真の図形がなぜ 1 1 2 Yahoo 知恵袋
ミラー指数による立方晶・六方晶における面と方向の表し方 前回の記事では結晶の基本構造について学んだ。 金属材料の変形を結晶の観点から理解するために、もうひとつ準備をしておきたい。 それは、結晶中の面や方向を表記する方法である。上線 = 負の数 (例) \( 1\overline{1}2 \) \( \ 1,\ {1},\ 2\ \) の数列。 下線 = 複数桁のグループ化 (例) \( 11\underline{12} \) \( \ 1,\ 1,\ 12
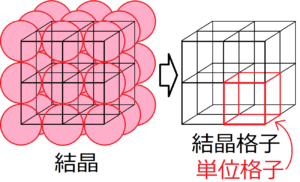



格子面とミラー指数の求め方




ミラー指数で表された面の図の書き方 化学徒の備忘録 かがろく 化学系ブログ



金属材料基礎講座 その24 ミラー指数の方向 ものづくりドットコム



ダイヤモンドの結晶と欠陥 中央宝石研究所 Cgl



2



ミラー指数



斜面に剛体の球を置いたときの球の運動はどのように計算できますか Quora



先進的な半導体開発のためのquantumatkの機能
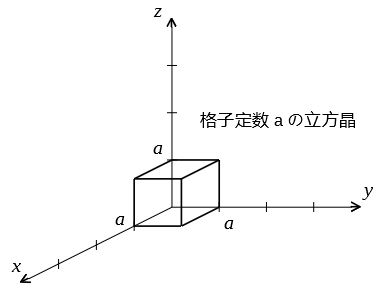



ミラー指数による立方晶 六方晶における面と方向の表し方




ミラー指数による立方晶 六方晶における面と方向の表し方
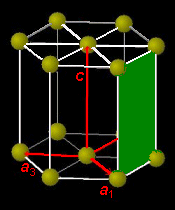



ときわ台学 結晶構造 ミラー指数



のミラー指数 方向指数 の求め方が分かりません 教えて下さい Yahoo 知恵袋




チョコ代引不可 Msciオリジナルマスクセット ハードケース付属 ファッション メンズファッション Www Writeawriting Com




Mate




ミラー指数による立方晶 六方晶における面と方向の表し方



1368円 初回限定お試し価格 リコピン 30日分 3個セット
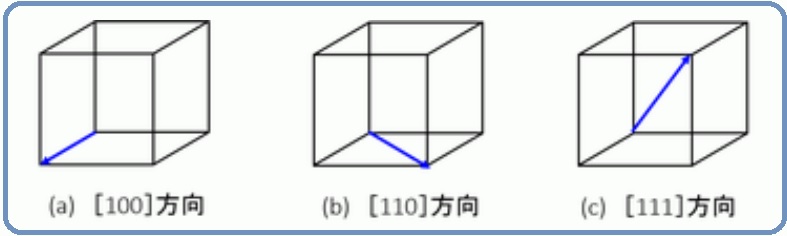



金属材料基礎講座 その24 ミラー指数の方向 ものづくりドットコム
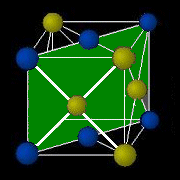



ときわ台学 結晶構造 ミラー指数




ミラー指数で表された面の図の書き方 化学徒の備忘録 かがろく 化学系ブログ



2




1155円 訳あり商品 トイレットペーパー ローズ0m巻芯無し 24巻



ミラー指数についての質問なのですが 方向の表し方が全然理解出来きません Yahoo 知恵袋



2
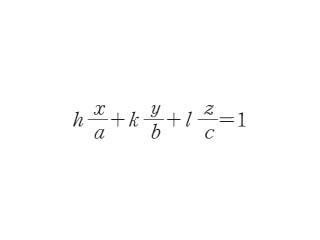



ミラー指数とは コトバンク



キーワード の検索結果 キーワード検索結果 透過電子顕微鏡 基本用語集 Jeol 日本電子株式会社



2



Hooktail Maxwell Jp




金属材料基礎講座 26 福﨑技術士事務所



ミラー指数の方向の問題です 何故このようになるのかさっぱりです 解き Yahoo 知恵袋



ミラー指数による立方晶 六方晶における面と方向の表し方



1



ミラー指数による立方晶 六方晶における面と方向の表し方




ミラー指数 天才エンジニアへの道
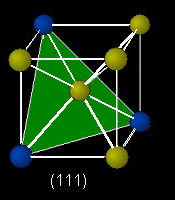



ときわ台学 結晶構造 ミラー指数
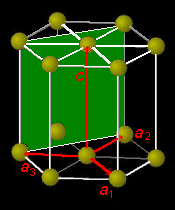



ときわ台学 結晶構造 ミラー指数



Power Focus 6000 ユーザーマニュアル




Unreal Engine において Windows で Ios をビルドする Unreal Engine ドキュメント




ミラー指数 Monozukuri Hitozukuri 日本のものづくり




ミラー指数 面指数 面を示すミラー指数 4つの整数のミラー指数 と方位指数 方位を示すミラー指数 化学徒の備忘録 かがろく 化学系ブログ



2



この画像のミラー指数は何かわかりますか またどのように求めたかも教 Yahoo 知恵袋



ミラー指数について質問です 六方晶の方位 12 13 が写真のようにな Yahoo 知恵袋
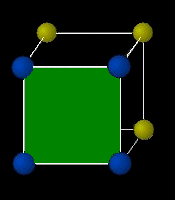



ときわ台学 結晶構造 ミラー指数
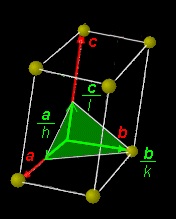



ときわ台学 結晶構造 ミラー指数



この図のミラー指数の解き方を教えてください 212 になるらしいのですが Yahoo 知恵袋
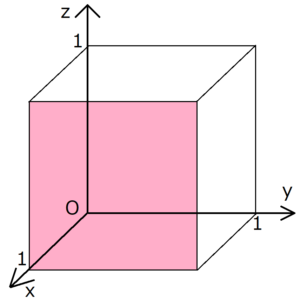



格子面とミラー指数の求め方



1
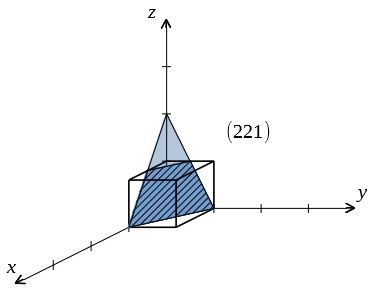



ミラー指数による立方晶 六方晶における面と方向の表し方
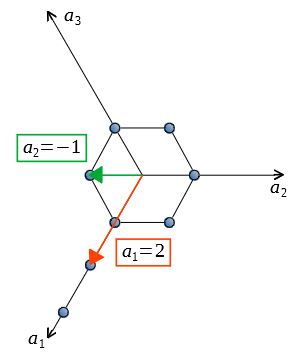



ミラー指数による立方晶 六方晶における面と方向の表し方
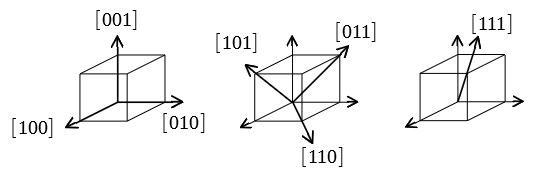



ミラー指数による立方晶 六方晶における面と方向の表し方



2




ミラー指数で表された面の図の書き方 化学徒の備忘録 かがろく 化学系ブログ



ミラー指数による立方晶 六方晶における面と方向の表し方



2



2




7 破面解析用語集 Monozukuri Hitozukuri 日本のものづくり



先進的な半導体開発のためのquantumatkの機能



2



この画像のミラー指数は何かわかりますか またどのように求めたかも教 Yahoo 知恵袋



2



2



ときわ台学 結晶構造 ミラー指数




ミラー指数による立方晶 六方晶における面と方向の表し方



Salvage Datasci Blogs Datasci Blogs Raw Csv At Master Yutannihilation Salvage Datasci Blogs Github



ときわ台学 結晶構造 ミラー指数



ミラー指数の方向の問題です 何故このようになるのかさっぱりです 解き Yahoo 知恵袋



ミラー指数 方向 物理のかぎしっぽ




ミラー指数 Monozukuri Hitozukuri 日本のものづくり



細胞培養肉の科学 このページは Good Food Instituteのsenior By Shojinmeat Project Shojinmeat Japan Medium



ミラー指数 Wikipedia



格子面とミラー指数の求め方



3



2



Jeans Ja En 0 5000 Txt At Main Cogcomp Jeans Github



のミラー指数 方向指数 の求め方が分かりません 教えて下さい Yahoo 知恵袋
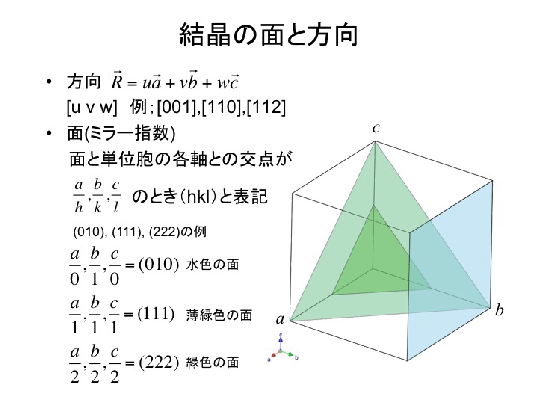



結晶の面と方向の記述方法



2



3
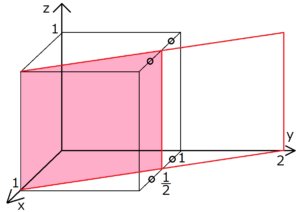



格子面とミラー指数の求め方



この図のミラー指数の解き方を教えてください 212 になるらしいのですが Yahoo 知恵袋




金属の結晶構造 ミラー指数 方向 面 Youtube
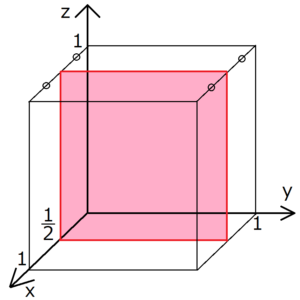



格子面とミラー指数の求め方




ミラー指数 天才エンジニアへの道




ミラー指数で表された面の図の書き方 化学徒の備忘録 かがろく 化学系ブログ



のミラー指数 方向指数 の求め方が分かりません 教えて下さい Yahoo 知恵袋
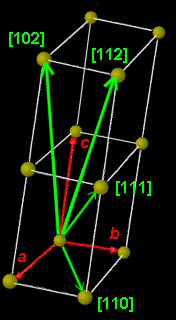



ときわ台学 結晶構造 ミラー指数




逆格子点の計算 Calculation Of Reciprocal Lattice And Reciprocal Lattice Points To Cause Diffraction
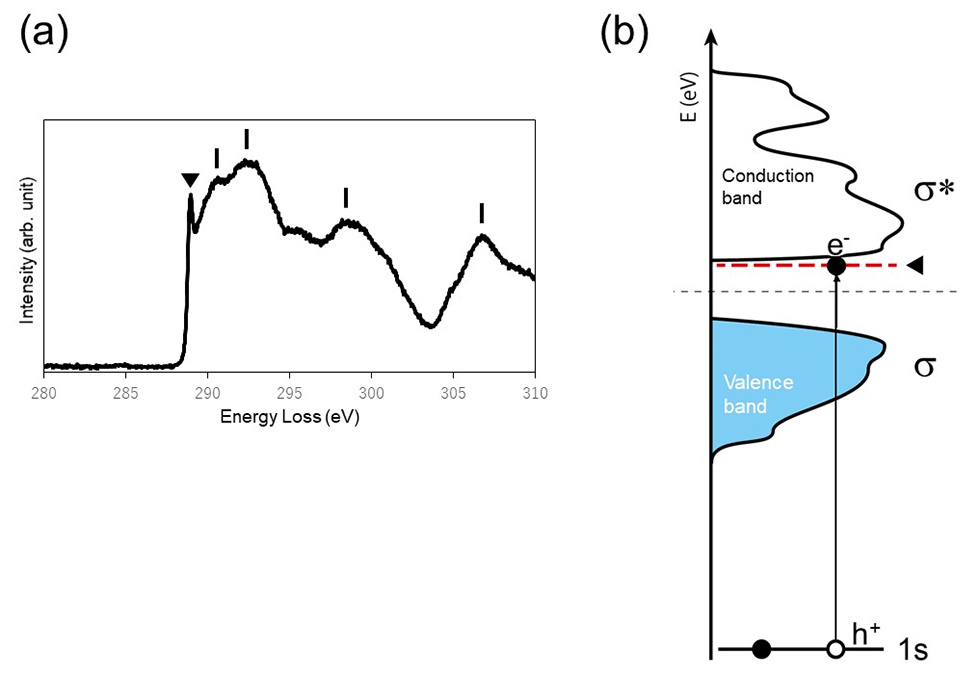



キーワード の検索結果 キーワード検索結果 透過電子顕微鏡 基本用語集 Jeol 日本電子株式会社
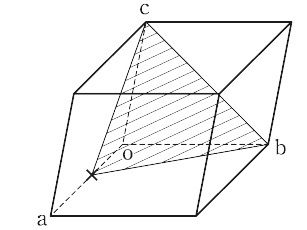



ミラー指数とは コトバンク



2



0 件のコメント:
コメントを投稿